De vorm van het universum kan bepaald worden door het meten van de gemiddelde dichtheid van de materie die erin zit, ervan uitgaande dat alle materie gelijk is verdeeld. Dit uiteraard afgezien van materieverdichtingen als sterrenstelsels. Deze veronderstelling wordt bijgestaan door de waarnemingen die op een gemiddelde homogeniteit en isotroopwaarde wijzen terwijl het universum toch vrij homogeen en anisotroop zou moeten zijn volgens de gangbare theorieën.
Veronderstellingen over de meetkunde van het universum kunnen in twee delen opgesplitst worden: de 'lokale' meetkunde die gerelateerd is aan het zichtbare heelal, en de 'globale' meetkunde die gerelateerd is aan het universum als een geheel, inclusief hetgeen we niet kunnen waarnemen.
Lokale meetkunde
De lokale meetkunde is de meetkunde die het gehele zichtbare universum omschrijft. Vele astronomische observaties zoals die van supernovae en de kosmische achtergrondstraling, tonen het zichtbare heelal als een homogene en isotroop en concludeert dat het versnelt. In algemene relativiteit wordt hier het Friedman-Lemaître-Robertson-Walker (FLRW) model gebruikt. Dit model kan voorgesteld worden door de Friedmann vergelijkingen die een lokale meetkunde van het universum beschrijven gebaseerd op wiskundige berekeningen van de bewegingen van vloeistoffen. Het stelt bijvoorbeeld de materie in het universum voor als een perfecte vloeistof. Sterren en structuren van massa kunnen ingepast worden in een "bijna FLRW" model, dit model wordt echter enkel gebruikt voor een grove berekening van de geometrie van ons universum.
Ruimtelijke kromming
In een homogeen heelal is het mogelijk om een constante 'kromming' te krijgen. Eén aspect van de lokale meetkunde van de algemene relativiteit en het FLRW model is dat de dichtheidsparameter, Omega Ω, gerelateerd is aan de kromming van de ruimte. Omega is de gemiddelde dichtheid van het universum gedeeld door de kritieke energiedichtheid. Bijvoorbeeld dat het vereist is dat het universum plat zou zijn (nulkromming, Ω = 0). Je kunt de kromming van de ruimte ook bekijken als een meetkundige omschrijving in welke mate de stelling van Pythagoras geldig is in die gekromde ruimte. In dit geval geeft het een alternatieve formule voor het uitdrukken van lokale relaties tussen afstanden.
Indien de kromming nul is, dan is Ω gelijk aan 1, en is de stelling van Pythagoras correct. Indien Ω > 1, dan is er een positieve kromming en als deze lager is dan 1 dan hebben we een negatieve kromming. In deze laatste gevallen is de stelling van Pythagoras dus ongeldig (Let wel: de afwijkingen worden alleen merkbaar als de lengte van de zijden een zeer grote schaal hebben). Als we de omtrek van cirkels van steeds grotere diameters meten en de eerste deelt door de tweede, zullen alle drie een waarde pi geven voor kleine diameters. Deze verhouding van pi stijgt echter voor grotere diameters, tenzij Ω = 1. Wanneer Ω > 1 (de bol op onderstaande figuur) zal de verhouding kleiner dan pi zijn, een grote cirkel op een bol heeft dan een omtrek die dubbel zo groot is als zijn diameter. Voor Ω < 1 zal de verhouding neerkomen op een waarde groter dan pi.
Astronomische metingen van beide materie-energie dichtheid van het universum en ruimtetijdsintervallen die gebruik maken van supernovagebeurtenissen beperken de ruimtelijke kromming tot zeer dicht bij 0, ook al is hier eigenlijk geen aanleiding voor. Dit betekent zoveel als dat we de vrij complexe ruimtetijd kunnen terugvoeren naar een driedimensionaal systeem.
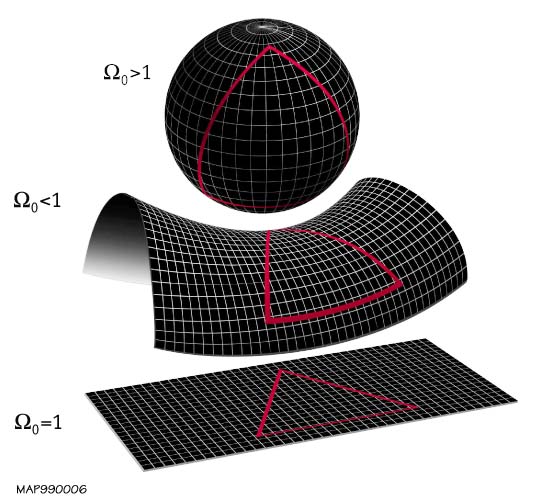
Lokale meetkunde
Er zijn drie vormen voor de mogelijke ruimtelijke meetkunde van constante kromming, afhankelijk van het teken van de kromming. Indien de kromming exact nul is dan is de lokale geometrie plat, is deze positief dan is de lokale meetkunde bolvormig en als ze negatief is dan is de lokale geometrie hyperbolisch.
Indien het zichtbare heelal ruimtelijk bijna plat is, dan kan een vereenvoudiging gemaakt worden waar de dynamica waarin de versnelling van de meetkunde gescheiden kan worden verworpen, kan worden door comoving coördinaten. Deze vormen één enkel referentiekader die een statische meetkunde geeft van drie ruimtelijke coördinaten.
Onder de veronderstelling dat het universum homogeen en isotropisch is, zou de kromming van het zichtbare heelal, of de lokale meetkunde, omschreven worden door één van de drie primitieve ruimteafmetingen:
- 3-dimensioneel euclidische meetkunde, afgekort als E3
- 3-dimensioneel sferische meetkunde met een kleine kromming, afgekort als S3
- 3-dimensioneel hyperbolische meetkunde met een kleine kromming, afgekort als H3
Zelfs als het heelal niet exact ruimtelijk plat is, zal de kromming erg dicht bij nul zijn en de straal nabij de horizon plaatsen van het zichtbare universum of verder.
Globale meetkunde
De globale meetkunde omvat de meetkunde, voornamelijk de topologie, van het gehele universum, zowel voor het zichtbare heelal als wat er verder ligt. De lokale meetkunde bepaalt nog niet volledig de globale meetkunde, het vermindert wel de mogelijkheden van vormen van het heelal, voornamelijk de meetkunde van een constante kromming. Voor een platte ruimtelijke meetkunde, is de schaal van elke eigenschap van de topologie willekeurig en kan daardoor niet detecteerbaar zijn. Voor sferische en hyperbolische ruimtelijke meetkunde is de kans dat de topologie gedetecteerd wordt door directe waarneming afhankelijk van de ruimtelijke kromming. Door de krommingsstraal te gebruiken als schaal, een kleine kromming van de lokale meetkunde, met een overeenkomstige schaal die groter is dan de zichtbare horizon maakt het moeilijk om de topologie te detecteren. Een sferische geometrie kan wel een straal hebben die gedetecteerd kan worden. In een hyperbolische meetkunde zal de straalschaal zich niet binnen de zichtbare horizon bevinden.
Twee sterk overlappende onderzoeken zijn bezig met het bestuderen van de globale meetkunde. De studie omvat:
- of het heelal oneindig in omvang is of een compacte ruimte is
- het heelal een eenvoudig of niet eenvoudig verbonden topologieheeft
Compactheid van de globale vorm
Een compacte ruimte is een algemene topologische omschrijving dat die het toepasselijke term van een begrensde metrische ruimte omvat. In kosmologische modellen is het vereist dat één of beide van de ruimte een positieve kromming heeft (zoals een bol) en/of meerdere verbindingspunten heeft, of beter gezegd: Niet eenvoudig verbonden.
Indien de verzameling van drie van een ruimtelijke sectie van het universum compact is, zoals bij een bol, zullen rechte lijnen richten in bepaalde richtingen en wanneer deze zich ver genoeg uitstrekken in dezelfde richting bereiken ze het startpunt en de ruimte een omschrijfbaar volume of schaal geeft. Indien de geometrie van het universum niet compact is dan is het oneindig in uitstrekking met oneindige paden van constante richting die niet terugkeren en de ruimte dus geen omschrijfbaar volume heeft zoals het Euclidische vlak.
Indien de ruimtelijke meetkunde sferisch is, dan is de topologie compact. Voor een platte of hyperbolische ruimtelijke meetkunde kan de topologie ofwel compact of oneindig zijn.
Plat heelal
In een plat heelal zijn alle lokale krommingen en lokale meetkunde vlak. Dit kan omschreven worden als de Euclidische ruimte, alhoewel is er sommige ruimtemeetkunde die in één of meerdere richtingen vlak en begrensd is. Deze omvatten, in twee dimensies, de cilinder en de torus. gelijkaardige ruimtes in driedimensionale ruimte bestaan ook.
Sferische heelal
Een positief gekromd heelal wordt omschreven als sferische meetkunde en kan aanzien worden als een driedimensionale hypersfeer.
Één van de doelstellingen in de analyse van data van de Wilkinson Microwave Anisotropic sonde WMAP is om meerdere "rug aan rug" beelden te detecteren van het verre heelal in de kosmische microgolf achtergrondstraling. Er van uitgaan dat het licht voldoende tijd had sinds haar oorsprong om rond een begrensd universum te reizen kunnen meerdere afbeeldingen waargenomen worden. Terwijl huidige resultaten en analyses niet wijzen in een richting van begrensde topologie,als het heelal begrensd is dan is de ruimtelijke kromming klein, net zoals de ruimtelijke kromming van het oppervlak van de Aarde klein is vergeleken met een horizon van duizend kilometer.
Hyperbolisch heelal
Een hyperbolisch heelal (regelmatig en verwarrend "open" universum genoemd) wordt omschreven als een hyperbolische meetkunde en kan gezien worden als iets als een driedimensionale equivalent van een oneindig uitgerekte zadelvormig heelal. Voor een hyperbolische lokale meetkunde zijn vele van de mogelijke driedimensionele ruimtes hoorntopologieën genoemd.
Het uiteindelijke einde van een open universum is dat het zich altijd zal blijven uitzetten en eindigen in een Big Rip, dovende hitte of grote bevriezing.








