De leeftijd van het universum is volgens de gangbare Big Bang theorie de tijd die verstreken is tussen het begin van het heelal en vandaag. De huidige wetenschappelijke consensus houdt de leeftijd van het heelal op 13,7 miljard jaar. Het meest conservatieve model van het universum geeft aan dat de tijd begint vanaf de Big Bang en speculeert niet wat er "voor" de Big Bang was.
Er zijn alternatieve mogelijkheden: in sommige kosmologische modellen (zoals het statische heelal of 'steady state' theorie) was er geen Big Bang en heeft het heelal een oneindige leeftijd. Toch is men het er tegenwoordig over eens dat waarnemingen de Big Bang theorie meer dan voldoende aantonen. Er zijn ook andere kosmologische modellen (zoals het cyclische model) waarin het universum altijd al heeft bestaan maar al meer reeksen van Big Bangs en Big Crunches heeft ondergaan. Indien men deze modellen behandelt, bedoelt men met de leeftijd van het heelal nog altijd de tijd van de laatste Big Bang tot nu.
Er is altijd een ambiguïteit in zowel de speciale als algemene relativiteit in precies het bepalen wat er met de tijd tussen twee gebeurtenissen bedoeld wordt. In het algemeen wordt de tijd gemeten door een klok, die echter afhankelijk is van de staat waarin ze zich bevindt. In de metrische FRW-methode (Friedmann-Robertson-Walker) die genomen wordt om het universum te beschrijven, is de aangewezen tijdsmeting de juiste tijdscoördinaat t die zich voordoet in het metrische.
De leeftijd gebaseerd op WMAP: (13.7 ± 0.2) × 109 jaar
Het universum is 13,7 miljard jaar oud met een foutenmarge van ongeveer 200 miljoen jaar. Deze leeftijd gaat er wel vanuit dat het onderliggend model juist is. Andere methoden om de leeftijd te bepalen, kunnen dan ook andere leeftijden geven. De berekening die wij behandelen, is gemaakt door de locatie te gebruiken van de eerste akoestische piek in de microgolfachtergrondstraling om de grootte van het universum te bepalen op het moment dat de atomen zich begonnen te binden. De reistijd van het licht tot deze regio (afhankelijk van de gebruikte meetkunde) geeft een goede schatting van de leeftijd van het universum, ervan uitgaande dat de geldigheid van de modellen die gebruikt werden voor de leeftijd te bepalen, een juistheid hebben binnen een marge van 1 procent. Deze waarde wordt door astronomen aanzien als de meest juiste.
Leeftijd in functie van kosmologische parameters
Het probleem bij het bepalen van de leeftijd van het universum hangt, dicht samen met het probleem van het bepalen van de waarden van de kosmologische parameters. Vandaag wordt deze meestal uit zijn context gehaald van het ΛCDM model waarin het universum normale materie, koude donkere materie, radiatie (inclusief neutrinos en fotonen) en een kosmologische constante bevat. De fractionele medewerking van ieder tot de huidige energiedensiteit van het universum, wordt gegeven door de dichtheidsparameters Ωm, Ωr en ΩΛ. Het volledige ΛCDM model is omschreven door een aantal parameters maar voor de bedoeling van het berekenen van de leeftijd zijn deze drie, samen met de Hubble parameter H0, het meest belangrijke.
Wanneer er accurate berekeningen zijn van deze parameters, kan de leeftijd van het universum bepaald worden door gebruik te maken van de Friedman vergelijking. Deze vergelijking relateert de graad van verandering in de schaalfactor met de materie-inhoud van het universum. Door deze relatie rond te draaien, kunnen we de verandering in tijd per verandering in schaalfactor berekenen en zo dus de leeftijd van het heelal bepalen door het invoegen van deze formule. De leeftijd t0 wordt dan gegeven door een expressie van de vorm:
![]()
Waar de functie F() enkel afhankelijk is van de fractie medewerking tot de energie-inhoud van het universum die uit diverse componenten komt. De eerste observatie die iemand uit deze formule kan halen is dat het de Hubble parameter is die de leeftijd van het universum controleert met een correctie voortkomende van de materie en energie-inhoud. Een ruwe schatting van de leeftijd komt dus van de inversie van de Hubble parameter:
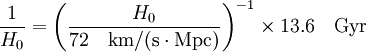
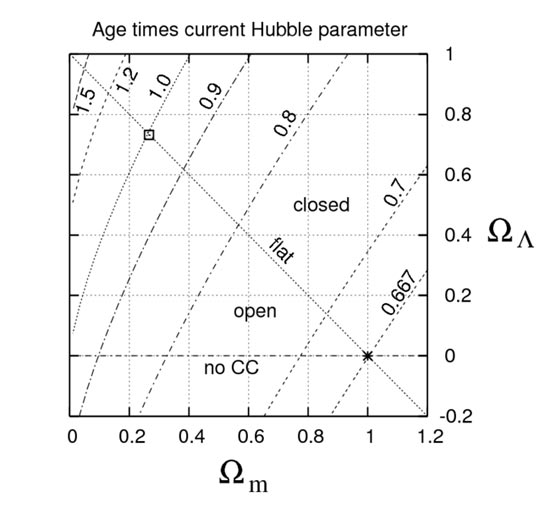
Om een preciezere waarde te verkrijgen, moet de correctiefactor F() berekend worden. In het algemeen moet dit numeriek gebeuren en het resultaat van een kosmologische parameterwaarde is getoond in bovenstaande figuur. Voor de WMAP waardes (Ωm,ΩΛ) = (0.266 , 0.732), getoond linksboven de figuur, is deze correctiefactor bijna gelijk aan 1: F = 0.996. Voor een plat universum zonder kosmologische constante, getoond door een de ster in de rechterbenedenhoek, F = 2/3 is veel kleiner en dus een veel jonger universum voor een aangepaste waarde van de Hubble parameter. Om deze figuur te maken, wordt Ωr constant gehouden. De krommingsdensiteitparameter is gefixeerd door de waarde van de andere drie.
Het Wilkinson Microwave Anisotropy Probe (WMAP) was bedoeld voor het berekenen van de leeftijd van het universum. CMB metingen zijn erg goed voor het bepalen van de materie-inhoud Ωm en de krommingsparameter Ωk.Het is niet zo gevoelig dan direct op ΩΛ, gedeeltelijk aangezien de kosmologische constante enkel van belang is bij lage roodverschuiving. De meest accurate bepalingen van de Hubble parameter H0 komen van het type SNIa supernovae. Deze metingen combineren leidt tot de algemeen geaccepteerde waarde van de leeftijd van het universum zoals hierboven vermeld.
De kosmologische constante zorgt ervoor dat het universum "ouder" lijkt voor gefixeerde waardes van de andere parameters. Voordat de kosmologische constante algemeen aanvaard werd had de Big Bang model moeilijkheden om uit te leggen waarom bolvormige sterrenhopen in de melkweg veel ouder leken te zijn dan de leeftijd van het universum wanneer men deze berekende met de Hubble parameter en een enkel materie bevattend universum. Door het introduceren van de kosmologische constante werd het universum ouder dan deze clusters en verklaarde ook andere zaken die het enkel materie bevattende kosmologische model niet kon verklaren.
Veronderstellingen
Het berekenen van de leeftijd van het universum is enkel precies als de veronderstellingen die ingebouwd zijn in de modellen ook juist zijn. Deze omvatten het wegwerken van mogelijke fouten in delen van het model om de juistheid weer te geven van actuele waargenomen data direct in het samenvattende resultaat. De leeftijd van het universum is gebaseerd op het 'best passende' op het WMAP datamodel 'enkel" is 13,4±0.3 Gyr (het ietwat hogere nummer van 13.7 bevat nog wat andere gegevens). Dit nummer geeft de eerste precieze directe meting van de leeftijd van het universum (andere methodes omvatten meestal de wet van Hubble en leeftijd van de oudste sterren uit bolvormige sterrenhopen...). Het is mogelijk om diverse methoden te gebruiken voor dezelfde parameter te bepalen (in dit geval de leeftijd van het universum) en uitkomen op een ander antwoord zonder overlapping in de 'fouten'. Om dit probleem te vermijden zijn er twee soorten van onzekerheden: de ene is gerelateerd aan de actuele meting en de andere gerelateerd aan de systematische fouten van het gebruikte model. Een belangrijk gedeelte van de analyse van de data om de leeftijd te bepalen (bvb op basis van WMAP) is de Bayesian Statistical analyse te gebruiken die de resultaten normaliseert boven bvb het model. Dit vermeerdert elke onzekerheid in de onjuistheid van een meting door het gebruik van een bepaald model.