In een system waar drie hemellichamen rond elkaar draaien, en waarvan één een verwaarloosbare massa heeft ten opzichte van de twee andere, zullen vijf punten voorkomen die voor dat lichtste object relatief stabiele punten zijn ten opzichte van de twee andere objecten. Deze punten zijn de Lagrangepunten of libratiepunten (van het Latijns voor evenwicht).
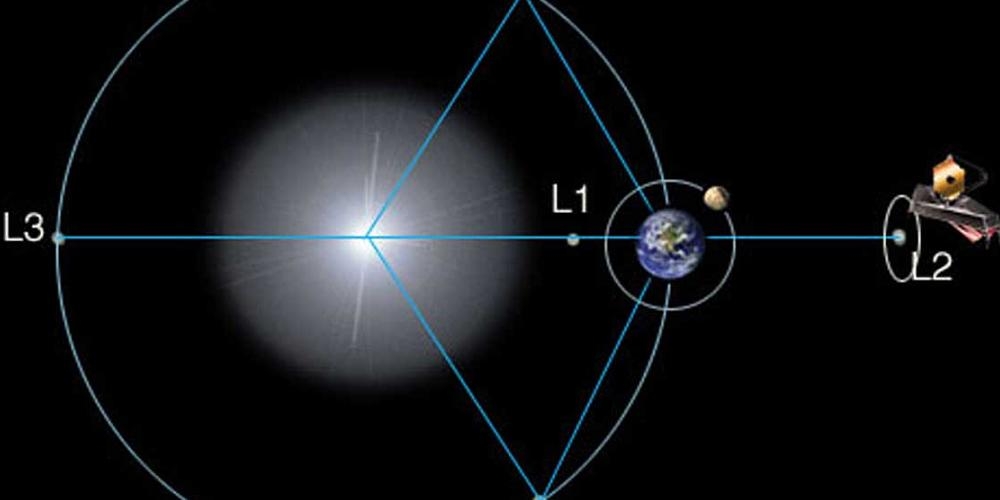
Meestal worden de twee zwaarste objecten aangeduid met A en B en is B ook een stuk lichter dan A. De Lagrangepunten krijgen de aanduiding L1 tot en met L5. Het zijn evenwichtspunten in het gravitatieveld van A en B, waar de gravitatie en A en B elkaar zowat opheffen. In het zonnestelsel kunnen de ‘zware’ objecten bijvoorbeeld de Zon en een planeet zijn of een planeet en een maan. Het derde object kan dan onder andere een andere maan, een planetoïde of een ruimtesonde zijn.
Het bestaan van de Lagrangepunten is een interessante uitwerking van het drie-lichamenprobleem. De punten zijn genoemd naar de Fransman Joseph Louis Lagrange (1736 - 1813) die het bestaan van deze evenwichtssituatie in 1772 aantoonde. Waar zijn de punten te vinden? De twee stabielste punten liggen op de baan van het lichtste object (B) van de twee zware en wel zo dat de verbinding van A, B en L4 enerzijds en A, B en L5 anderzijds een gelijkzijdige driehoek vormen met hoeken van 60° (zie afbeelding). De punten L4 en L5 bevinden zich dus even ver van A als van B. Deze twee punten worden ook de driehoekspunten genoemd. De drie andere punten zijn L1 tot en met L3, ook de colineaire punten, en liggen op de verbindingslijn tussen A en B. Objecten op die punten ondervinden storingen. Van zodra ook maar een beetje van het evenwichtspunt wordt afgeweken zal de afwijking alleen maar groter worden (als er niet wordt gecorrigeerd). Bij de Zon en een planeet bevindt het punt L4 zich 60° vóór en L5 60° achter de planeet op dezelfde baan als de planeet. Bij afspraak gaat het punt L4 het object B vooraf, en volgt L5 op B.
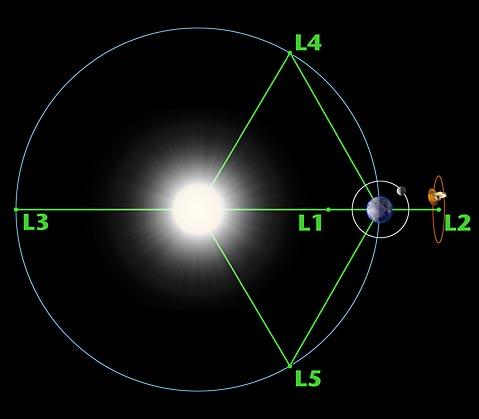
In L4 en L5 van het Zon-Jupitersysteem bevinden zich de Trojanen. De ontdekking van Trojanen was een schitterende bevestiging van de theorie van Lagrange. De eerste, 588 Achilles, werd ontdekt in 1906 op L4. Trojanen zijn planetoïden die rond de Zon draaien in een periode van ongeveer 11 jaar (de omlooptijd van Jupiter). Ze hebben geen vaste positie ten opzichte van de punten L4 en L5, maar voeren er een beweging rond uit in 150 tot 200 jaar. Vanuit ons standpunt is de hoek tussen een Trojaan en Jupiter gemiddeld dus 60°, maar dat varieert tussen 45° en 80°. De groep planetoïden op het punt L4 werd ook soms de Grieken genoemd, maar tegenwoordig gebruikt met de naam Trojanen voor alle planetoïden op L4 én L5 van elk system van de Zon en een planeet. Ook Mars, Saturnus, Uranus en Neptunus hebben enkele Trojanen, maar alleen Jupiter heeft er duizenden. Op 12 februari 2010 waren 2.603 Trojanen bekend op L4 (63,86%) en 1.473 op L5 (36,14%). Trojanen kunnen toch soms uit hun positie ontsnappen en een andere baan in het zonnestelsel aannemen, of omgekeerd. Een Trojaan is dat dus niet per definitie voor altijd.
Dat het vinden van Trojanen niet altijd eenvoudig is bewijst de ontdekking van de eerste en enige Trojaan op het punt L5 van Neptunus (en de Zon). In augustus 2010 kondigden Scott Sheppard (Department of Terrestrial Magnetism) en Chad Trujillo (Gemini Observatory) de ontdekking aan van 2008 LC18 die dus al in 2008 is gespot. Het punt L5 van Neptunus ligt zo’n 60° achter Neptunus op zijn baan. Dat is nu toevallig in de buurt van het centrum van het Melkwegstelsel. Tussen al de sterren daar een object ontdekken dat iets met Neptunus te maken heeft is geen sinecure. Alle vorige Trojanen bij Neptunus werden op L4 gevonden. Ook van Neptunus vermoedt men dat er vele duizenden Trojanen bestaan, maar op L4 en L5 samen zijn er nog maar acht ontdekt (op 12 februari 2010).

In het stelsel Aarde-Maan zijn de punten L1 en L2 gelegen op ongeveer 60.000 km van de Maan. L1 ligt tussen de Aarde en de Maan, L2 ligt steeds ‘achter’ de Maan. Het punt L3 ligt circa 400.000 km van de Aarde, aan de andere kant van waar de Maan te vinden is (alleen bij Volle Maan dus tussen de Aarde en de Zon). De punten L4 en L5 liggen op de baan van de Maan, telkens zo’n 400.000 km van de Aarde en de Maan.
Op een ‘lager’ niveau bestaan ook Lagrangepunten tussen een planeet en een maan. Op het punt L4 van het systeem Saturnus-Dione bijvoorbeeld is de maan Helene te vinden. Veralgemeen echter niet dat op elke L4 of L5 van een planeet en een grote maan een kleinere maan te vinden is. In de stabiele lagrangepunten van het Aarde-Maansysteem bevinden zich mogelijk de Kordylewskiwolken. In 1956 meende de Poolse sterrenkundige Kazimierz Kordylewski objecten te hebben gevonden op de punten L4 en L5. Hij beweerde ze in 1961 zelfs gefotografeerd te hebben, maar tot op heden is niets met zekerheid op die punten gevonden.
Ruimtesondes voor onderzoek van de Zon worden soms rond het punt L1 van het Zon-Aardesysteem geplaatst, dat zich op een afstand van circa 1,5 miljoen km van de Aarde, tussen de Aarde en de Zon, bevindt. Er moet echter voortdurend bijgestuurd worden om de ruimtesonde op zijn plaats te houden: een minieme afwijking zal in de loop van de tijd alleen maar groeien. Om dat op te lossen wordt de ruimtesonde in een baan om het libratiepunt gebracht: een halo-baan. De eerste ruimtesonde in een Halo-baan rond L1 was de International Sun-Earth Explorer 3 (van 1978 tot 1982). Daarna verliet hij de plaats en bezocht hij de komeet Giacobini-Zinner. Andere voorbeelden zijn de Solar and Heliospheric Observatory (SOHO), Wind, Advanced Composition Explorer (ACE) en Genesis. Op het punt L2 zijn ook ruimtesondes te vinden zoals de Wilkinson Microwave Anisotropy Probe (WMAP was de eerste), de Herschel Space Observatory en Planck. In de toekomst zullen onder andere GAIA en de James Webb Space Telescope van daar observeren. Een bijzondere missie is Stereo: de twee sondes voor deze missie werden in de punten L4 en L5 geplaatst en hebben zo een bijzonder zicht op de Zon. Ruimtesondes die in de buurt van L1 aankomen worden in een halo-baan gebracht, aangeduid als L1LO. Een L1LO-baan ligt in een vlak dat een hoek vormt met de ecliptica en is elliptisch (zie afbeelding 1). De diameter van de Halo-baan is enkele honderdduizenden kilometers en de ruimtesonde op deze baan doet er vele maanden over om deze eenmaal te doorlopen. Voor SOHO bijvoorbeeld is dat 180 dagen.
Libratiepunten kunnen ook heel dicht bij het object B liggen. In het geval van Mars en Phobos liggen de libratiepunten L1 en L2 op slechts 4,2 km van het oppervlak van Phobos. De posities van de punten L1 tot en met L3 hangt af van de massa van A en B, maar de posities van L4 en L5 zijn onafhankelijk van de massa van 1 en B. Enige voorwaarde om van de punten L4 en L5 stabiele punten te maken is dat de massa van A minstens 24,96 keer groter is dan deze van B.