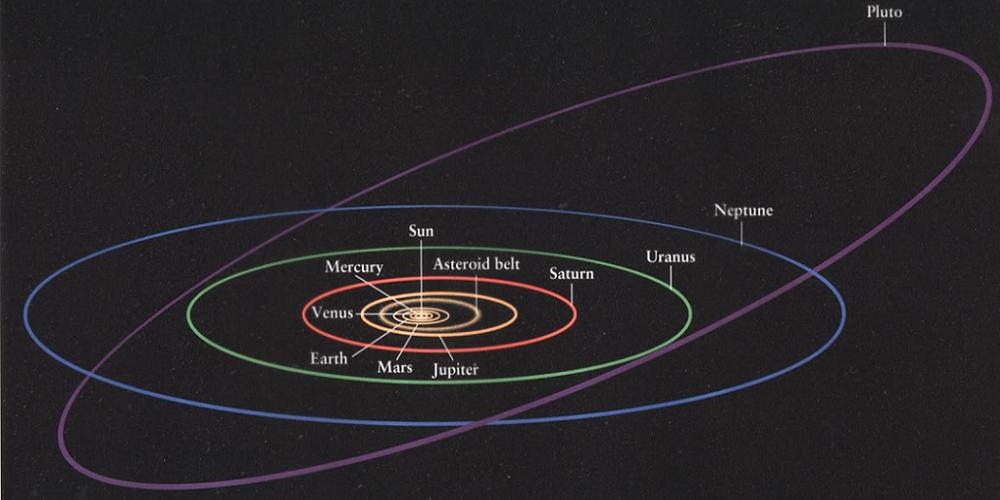
Johannes Kepler ontdekte in de 16de eeuw aan de hand van waarnemingen van de planeet Mars dat alle planeten in ons zonnestelsel in ellipsvormige banen rondom de zon draaien. Deze ellipsen zijn uitgestrekte cirkels die in tegenstelling tot de cirkel, niet één maar twee brandpunten hebben. De excentriciteit is de maat voor te bepalen hoeveel de vorm van een ellips afwijkt van die van een cirkel.
Zo zullen objecten met een langgerekte elliptische baan een excentriciteit hebben die hoger is dan een baan die bijna identiek aan een cirkel is. Excentriciteit wordt in de wis-, natuur- en sterrenkunde afgekort door de letter e. Een elliptische omloopsbaan kent een periapsis en een apoapsis. Dit zijn de algemene benamingen van de kleinste (periapsis) en de grootste (apoapsis) afstand van een hemelobject tot zijn baan. Deze twee eenheden kunnen vergeleken worden met het perihelium en het aphelium van een baan. Wanneer deze twee gegevens gekend zijn, kan men de excentriciteit van de ellips bepalen.
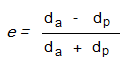
Waarbij:
- da = de apoapsis in astronomische eenheden (AE)
- dp = de periapsis in astronomische eenheden (AE)
Dus om de excentriciteit van de aarde te berekenen:
Gegeven:
- da = 1,02
- dp = 0,98
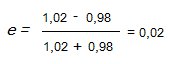
De werkelijke excentriciteit bedraagt 0,016710219, maar doordat de gegevens van de periapsis en de apoapsis slechts op twee cijfers na de komma zijn gegeven, komt men uit op een afgerond getal, nl. 0,02. Dit is een dichte benadering van de werkelijke excentriciteit.
Het zou kunnen dat je bij gebruik van deze formule een negatief getal bekomt. Indien dit voorkomt geldt:
e = |e|
Dit wil zeggen dat je de absolute waarde van het berekende resultaat moet nemen. De absolute waarde is gelijk aan de positieve vorm van een getal. Ook van andere kegelsneden verschillend van de ellips kan de excentriciteit bepaalt worden. Bij een cirkel is de excentriciteit gelijk aan 0, bij een ellips is de excentriciteit gelegen tussen 0 en 1. Een parabolische baan (een oneindig lang-gerekte ellips) heeft een excentriciteit van precies 1, terwijl een hyperbolische baan een excentriciteit groter dan 1 heeft.